The apocalypse problem
I’ve recently been going through the book Cracking the coding interview (6th ed.), and an interesting problem was stated there (abridged for brevity):
In a new post-apocalyptic world, the world leader decides that all families must have one girl, or face massive fines. If all families continue to have children until they have one girl, at which point they immediately stop, what will the gender ratio of the new generation be? Assume that the probabilities of having a boy or a girl are equal.
The solution
Since all families must eventually have exactly one girl, then $N_\text{girls} = N$, where $N$ is the number of families. The probability of having $n$ boys (denoted $B$) before having a girl (denoted $G$) is therefore:
\[P(\underbrace{BB\ldots B}_{n}G) = \underbrace{\frac{1}{2}\times\frac{1}{2} \times \cdots \times \frac{1}{2}}_{n} \times \frac{1}{2} = \frac{1}{2^{n + 1}}\]While we don’t know exactly how many boys are in each individual family, we can still compute the average, or the expectation value, of the number of boys in a family, defined as:
\[\mathbb{E}(X) = \sum_{n}x_n\, p_n = \sum_{n=0}^\infty\frac{n}{2^{n + 1}} = \frac{1}{2} \times \sum_{n=0}^\infty\frac{n}{2^{n}}\]where we’ve taken the random variable $X$ to be the number of boys in a family, hence $x_n = n$ and $p_n = 1/2^{n + 1}$, and the sum goes over all possibilities ($[0,\ldots,\infty)$ boys)1.
How do we compute this sum without a computer? Well, let’s first consider the following sum instead:
\[S_n (q) = \sum_{i = 0}^n q^i\]This is the well-known geometric sum, whose sum is equal to2:
\[S_n (q) = \frac{q^{n + 1} - 1}{q - 1}\]We can see that, for $0 < q < 1$, we have the following:
\[\lim_{n \rightarrow \infty} S_n(q) = \lim_{n \rightarrow \infty} \sum_{i = 0}^n q^i = \lim_{n \rightarrow \infty} \frac{q^{n + 1} - 1}{q - 1} = \frac{1}{1 - q}\]The reason is that, since $0 < q < 1$, we have that $q^2 < q < 1$, etc., and in fact the entire sequence $\left\lbrace 1, q, q^2, \ldots \right\rbrace$ is decreasing, and since it’s bounded below by 0, it means that we have $\displaystyle\lim_{n \rightarrow \infty} q^n = 0$, which gives the above. We may as well define:
\[S(q) = \sum_{i = 0}^\infty q^i = \frac{1}{1 - q}\]to keep things concise. Now, how does this apply to our problem? Well, if we put $q = 1/2$ in the above, we get:
\[S\left(\frac{1}{2}\right) = \sum_{i = 0}^\infty \left(\frac{1}{2}\right)^i = \frac{1}{1 - 1/2} = 2\]Now, if we compute the first derivative of $S(q)$, on the right-hand side we get:
\[\frac{\text{d}}{\text{d} q}S(q) = \frac{1}{(1 - q)^2}\]while the left-hand side is just:
\[\frac{\text{d}}{\text{d} q}S(q) = \sum_{i = 1}^\infty i\, q^{i - 1} = \sum_{i = 0}^\infty (i + 1)\, q^i = \sum_{i = 0}^\infty i\, q^i + \sum_{i = 0}^\infty q^i\]where in the last step we’ve just split one sum into two. However, you may notice that the second term is actually just $S(q) = 1/(1 - q)$, so we have:
\[\sum_{i = 0}^\infty i\, q^i = \frac{1}{(1 - q)^2} - \frac{1}{1 - q} = \frac{q}{(1 - q)^2}\]where we’ve simplified the final expression with a bit of algebra. But the expression on the left-hand side is exactly what we’re looking for, provided we take $q = 1/2$! Therefore, going back to the original problem, we have that:
\[\mathbb{E}(X) = \frac{1}{2} \times \sum_{n=0}^\infty\frac{n}{2^{n}} = \frac{1}{2} \times \frac{1 / 2}{(1 - 1 / 2)^2} = 1\]This result may be a bit puzzling: it seems that the policy of the world leader is completely useless, since in the end we just end up with 1 boy and 1 girl per family, on average. But recall that biology hasn’t been altered, so we sort of expect that things would even out.
Going beyond: unequal probabilities
What happens if the probabilities are not equal though? Let’s say the probability of having a boy is $p$; then the probability of having a girl would be $1 - p$, and the probability of having a girl after $n$ boys is now:
\[P(\underbrace{BB\ldots B}_{n}G) = \underbrace{p\times p\times\cdots\times p}_{n}\, (1 - p) = p^n\, (1 - p)\]Then the expectation value for the number of boys is:
\[\mathbb{E}(X) = \sum_{n=0}^\infty n \times p^n (1 - p) = (1 - p) \sum_{n=0}^\infty n \times p^n = (1 - p) \times \frac{p}{(1 - p)^2} = \frac{p}{1 - p}\]From this we can see that the original problem is just the special case $p = 1/2$. I’ve plotted the expectation value of the number of boys as a function of the value of $p$ below.
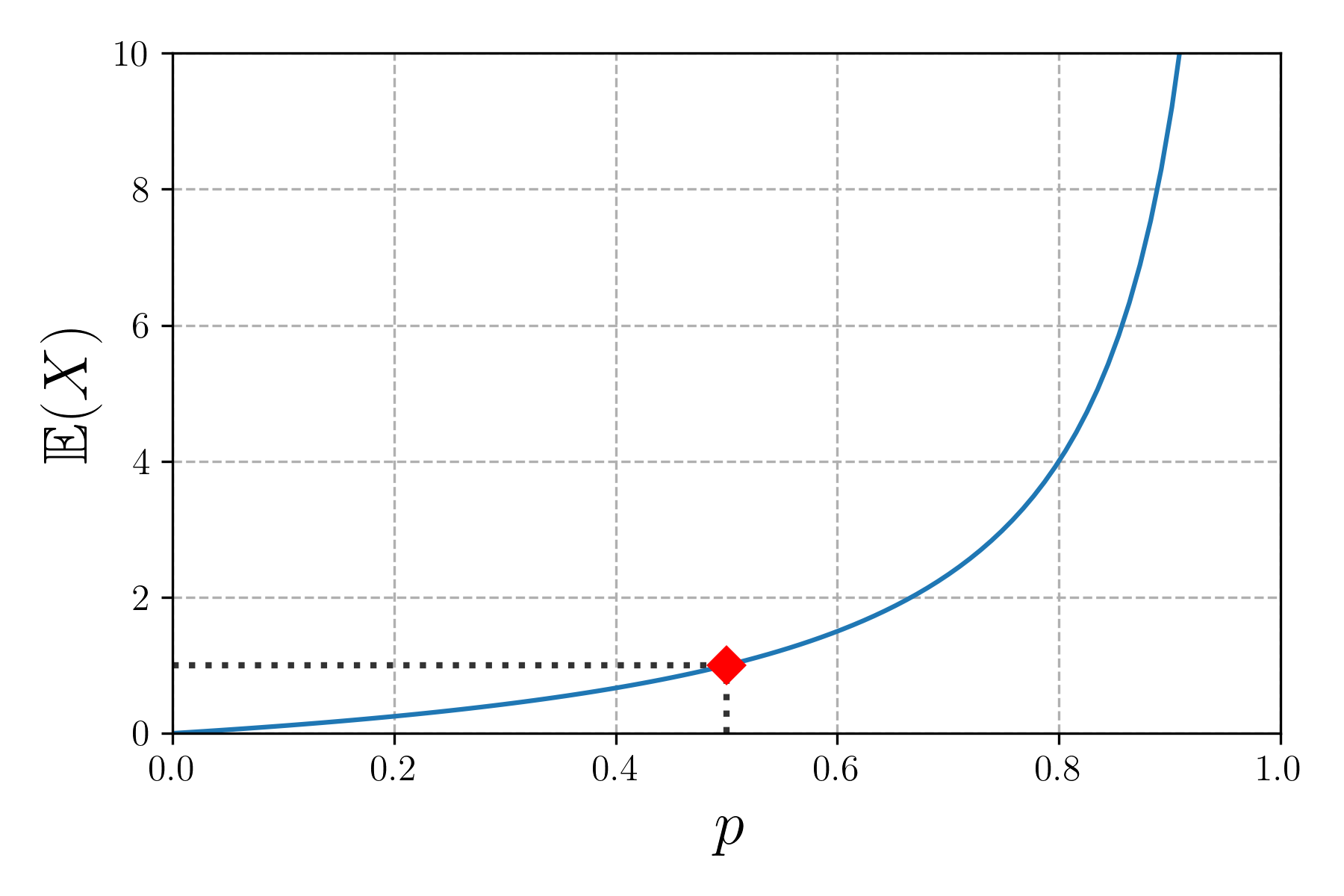The number of boys as a function of the value of $p$. The red diamond represents the special value $p = 1/2$, for which the expectation value is 1.
It’s worthwhile to note that an equivalent problem is to consider $N$ (in the general case, biased) coins, which we keep flipping until we get one of the outcomes, say, heads. Actually, we don’t even need $N$ coins; since the coin flips are statistically independent, we may as well keep throwing the same coin until we get heads, and then repeat this procedure $N$ times.